Analítica de Marketing: Segmentación de Mercados

Marketing STP

La segmentación de mercado es la primera fase del marketing STP (abreviaturas en inglés para Segmentation, Targeting y Positioning). El marketing STP, implica establecer los segmentos correctos para comercializar tu producto (Segmentación). Identificando el mercado objetivo adecuado (Focalización) y posteriormente posicionando el producto para recibir el máximo beneficio (Posicionamiento). Un aspecto importante del marketing STP es determinar los beneficios que tu producto ofrece y quiénes se beneficiarán al utilizarlo.

El primer paso del marketing STP es la segmentación del mercado. Para encontrar esos segmentos utilizaremos el Marketing Analytics, y la primera pregunta que debemos responder es: ¿Cuáles son las maneras de segmentar un mercado?

La segmentación de mercado puede basarse en diferentes aspectos: factores demográficos, psicográficos y geográficos. Por ejemplo, una universidad puede dividir sus clientes entre alumnos de pregrado y alumnos de postgrado, de manera de dividir sus esfuerzos de marketing en estos dos grupos.

Pero ¿cuales son beneficios de la segmentación de mercados?. Los diferentes segmentos tienen diferentes necesidades, por lo que las empresas necesitan desarrollar diferentes mensajes para cada segmento, esto incrementa la satisfacción de sus cliente al dirigirse a necesidades más específicas con los segmentos individuales del mercado que con el mercado general. la figura siguiente muestra un resumen de las principales ventajas de la segmentación de mercado.

Los enfoques de segmentación de mercado se pueden dividir en dos grupos; A priori y las Post Hoc. El enfoque a priori se refieren a los segmentos definidos antes de la investigación o análisis del mercado y las post hoc que son los segmentos definidos después del análisis del mercado.

En cuanto a las técnicas de segmentación la podemos dividir en dos grupos: descriptivas y predictivas. Las técnicas descriptivas describen las similitudes y diferencias entre los grupos y las técnicas predictivas se utilizan para predecir la relación entre las variables independientes y dependientes. Un resumen de las diferentes técnicas y sus categorías la podemos ver en la siguiente figura.

Hasta ahora hemos definido lo que significa la segmentación, pero ¿ Cómo se lleva a cabo el análisis de conglomerados o un análisis de la segmentación?. Existen muchas técnicas de agrupamiento, en este post voy a explicar dos técnicas y el objetivo de cada uno de éstas es formar grupos y estos grupos deben ser similares con respecto a los criterios que se está utilizando para segmentar el mercado dentro de un grupo, pero son diferentes a los otros grupos o segmentos.

Hierarchical Clustering

Esta técnicas es una de las más populares para la segmentación del mercado. Es un procedimiento numérico que intenta separar un conjunto de observaciones en grupos de abajo hacia arriba uniendo individuos secuencialmente hasta que obtengamos un grupo grande. Por lo tanto, esta técnica no requiere la especificación previa del número de grupos que queremos sementar, para el ejemplo utilizaremos el lenguaje R, un lenguaje muy común para el análisis de datos.

Primero importamos un conjunto de datos, en este caso una encuesta donde se le preguntan a estudiantes de MBA y Pregrado las características que debe tener un auto de lujo en términos de: estilo, moderno, fiabilidad, deportividad, rendimiento y comodidad en donde se le asigna un porcentaje a cada característica.

Antes de ejecutar el algoritmo hay que asegurarse que las variables tengas las mismas escalas, en este paso lo que necesitamos es la estandarización de la variable sobre todo si se miden con diferentes escalas, para ello seleccionamos las variables númericas y le aplicamos una distancia euclidiana.

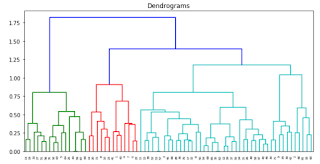
Ahora usamos la función hclust () para aplicar la agrupación jerárquica en nuestros datos. Utilizamos el criterio Ward que tiene como objetivo minimizar la varianza dentro del grupo. Obtenemos el siguiente dendograma que puede ayudarnos a decidir el número de clústeres a retener.

Según el dendograma pareciera haber 3 o 4 grupos. Analizando con 4 grupos el primer grupo tiene 18 personas, el segundo grupo 29 personas, el tercer grupo 17 personas y el cuarto grupo sólo nueve personas. Si analizamos con 3 grupos pareciera que todos los del grupo cuatro se fueron al grupo uno, dejando sin modificaciones los grupos dos y tres.

Al parecer tres grupos es la cantidad de segmentos indicados, esta solución parece tener grupos de tamaños similares. Además, podemos caracterizar fácilmente cada uno de ellos. El primer grupo se preocupa por el rendimiento y la fiabilidad, mientras que el segundo grupo valora la comodidad y la deportividad, finalmente, el tercer grupo se preocupa por la apariencia, tal como lo muestra la figura siguiente:

Dado lo anterior, podemos agrupar los grupos por rendimiento, comodidad y apariencia. Un buen criterio para poder identificar a las personas que se encuentran de estos grupos es analizar las variables demográficas, este en este caso nuestra única variable demográfica es si el alumno es estudiante de MBA o de Pregrado, por lo tanto utilizaremos la técnica de CrossTable para analizar esta variable.

La tabla siguiente muestra en sus columnas, los tres grupos que se han encontrado a partir de la técnica Hierarchical Clustering, y las filas son el tipo de estudiante (MBA, Pregrado).

La tabla muestra que hay 24 estudiantes de MBA que representan el 33% de la muestra y 49 estudiantes de Pregrado que representan el 67% del total. Para los estudiantes de MBA 14 de los 24 estudiantes pertenecen al segmento de rendimiento, ósea un 58%. Por lo tanto, los estudiantes de MBA parecen más propensos a preferir un auto con mayor rendimiento. Por otra parte los estudiantes de pregrado 23 de ellos, ósea el 47% se ubica en el segmento de la comodidad, por lo que sus preferencias parecieran enfatizar en estilo y comodidad.

Es importante en la segmentación de mercado no perder el objetivo estratégico, para esto debemos responder la siguiente pregunta ¿ Los segmentos identificados nos conducen a diferentes estrategias de mercado? la segmentación de mercado es la búsqueda y la comprensión de los drivers de elección y las opciones que están disponibles para los consumidores. Al parecer según nuestro análisis nuestros drivers de elección son el rendimiento, comodidad y apariencia y las opciones disponibles son las marcas de los autos: BMW, Mercedes y Lexus. Por lo tanto esperamos que exista una relación entre los drivers y las opciones de compra. Aplicando la técnica CrossTable para comprar estas dos dimensiones obtenemos lo siguiente: 14 de las 27 personas del grupo de rendimientos eligieron BMW lo que representa un 52%, para el caso de la comodidad el 37% eligió Mercedes y 34% eligió BMW por lo que este grupo se encuentra divido entre estas dos marcas. Para el grupo de la apariencia el 43% eligió BMW por lo que esta marca parece ser atractivo en todos los segmentos

K-means Clustering

Ahora nos centramos en un método diferente llamado K-means. Este método nos obliga a especificar con antelación el número de grupos, sabemos por nuestro análisis anterior que tres grupos es el número más adecuado. Aplicando el algoritmo para tres grupos en esencia nos muestra las mismas agrupaciones de rendimiento, comodidad y apariencia, además nos muestra al individuo y su grupo correspondiente, así el individuo 1 tiene asignado el grupo 1, el individuo 2 tiene asignado el grupo 1 y así sucesivamente.

En este post intenté dar una visión general de la segmentación del mercado, también mostrar dos de las técnicas más utilizadas para la segmentación como lo son Hierarchical y K-means. Si bien estas técnicas son de gran utilidad para entender nuestros datos de clientes, el analista siempre debe darle una interpretación de negocio a los resultados y asegurarse que los grupos encontrados tengan sentido para las estrategias de marketing, al final esto no es una ciencia, es más un arte y el criterio del analista será muy importante en los análisis de segmentación.

Vendedor viajero: Algoritmos Hill Climbing y A*

Descripción

Este post intenta explicar el problema del vendedor viajero con los algoritmos Hill Climbing y A*. Lo hice hace mucho tiempo, espero les sirva….

Un viajero debe visitar n ciudades, no debe pasar por una ciudad mas de una vez y retornar a la ciudad de donde partió, la distancia entre cada ciudad tiene un peso, el problema es encontrar la distancia mínima de la ruta para visitar todas las ciudades sin pasar por una mas de una vez

Para exponer este tipo de problema se especifica lo siguiente:
Sea N ciudades de un territorio. La distancia entre cada ciudad viene dada por la matriz Peso: NxN, llenada aleatoriamente, donde d[x,y] representa la distancia que hay entre la ciudad X y la ciudad Y. El objetivo es encontrar una ruta que, comenzando y terminando en una ciudad concreta, pase una sola vez por cada una de las ciudades y minimice la distancia recorrida por el viajante.

Por tanto a cada ciudad se le asignara un peso, que representara la distancia de una cuidad con la otra, estos valores se guardaran una matriz peso
Llenado de la matriz Peso

	1	2	3	4
1	0	1	79	65
2	1	0	56	6
3	79	59	0	46
4	65	6	46	0

int aleat() Matriz de peso para N=4
{
return ((rand()%100)+1);
}
for (i=1;i<=n;i++)
for(j=1;j<=n;j++)
{
peso[i][j]=-1;
if (i==j)
{
peso[i][j]=0;
}
else
{
num_aleat=aleat();
peso[i][j]=num_aleat;
peso[j][i]=num_aleat;
}
}
La solución más directa es la que aplica la fuerza bruta: evaluar todas las posibles permutaciones y quedarse con la mejor. No obstante, el número de posibles ciclos viene dado por el factorial del número de ciudades (N!) y esto hace que la solución por fuerza bruta sea impracticable para valores de N incluso moderados. Por ejemplo, si un ordenador fuese capaz de calcular la longitud de cada ciclo en un microsegundo, tardaría algo más 3 segundos en resolver el problema para 10 ciudades, algo más de medio minuto en resolver el problema para 11 ciudades y... 77.146 años en resolver el problema para sólo 20 ciudades.
Generación de árbol de caminos
Para generar el árbol de caminos utilizamos 4 Arreglos con nombres:
Ciudad[N][N] = que guarda el árbol de todas las posibles rutas del viajero.
Nodo[N][N] = que contiene el nombre de cada nodo de la matriz ciudad.
Padre[N][N] = que contiene el Padre de cada nodo de la Matriz Ciudad
Cola [N] = Este vector va guardando el padre de los nodos generados,
lo que nos permitirá ir creando el árbol de caminos.
Árboles para N=4 y Ciudad inicial 2

Árbol Ciudad Árbol Nodo




Árbol Padre
Estas 3 matrices nos permitirán movernos a trabes del árbol de caminos por medio del vector cola, este vector adquiere los valores de la función
generar_cola(), la cual junto con la función generar_padre() va buscando el padre de los nodos por medio de la matriz padre.

Código para la generación del Árbol de caminos

while (contador < en-1)

{

num=len(i); // devuelve el numero de nodos del nivel i

for(k=1;k<=num;k++) // ciclo que genera cantidad de hijos

{

nodo[i][k]=var; // llena la matriz nodo con valores

var++; sucesivos 1,2,3…..,n

generar_cola(i,k); // genera el camino recorrido

valor_cola(); // recupera el nombre original del nodo

for(m=1;m<=n;m++) // genera los hijos

{

for(h=1;h<=i;h++) // busca hijos en cola

if(cola[h]==m) valor=1; // si el nodo esta en

if(valor==0) cola valor=1 entonces

{ se salta el nodo

ciudad[i+1][j]=m; //guarda la matriz ciudad

padre[i+1][j]=nodo[i][k]; // matriz padre

j++;

}

valor=0;

}

}

i++;

j=1;

contador++;

}

Una vez creadas las 3 estructuras, podremos implementar nuestro algoritmo de búsqueda.
Algoritmo de Hill Climbing

Esta búsqueda se puede implementar en nuestro algoritmo como una estructura de dato tipo pila, en la cual se van guardando los hijos de los nodos revisados, así por ejemplo, se revisa primero el nodo 1, el cual se guarda en la pila.

1

0

0

0

0

Luego se revisa a sus hijos (2 y 3),
Se ordenan de menor a mayor de acuerdo
Al peso que ellos poseen, sea el peso del
Nodo (2)=75 y Nodo (3)=60, quedaría ordenados
De forma 3,2, luego Se guardan en la pila
los hijos ordenados para posteriormente revisar
los hijos del primer elemento de la pila

3

2

1

0

0

Luego como 1 ya no tiene más hijos sin revisar
Se elimina el vector cola y se revisan los hijos
De 3

3

2

0

0

0

5

4

3

2

0

Si 5 es el elemento buscado termina la búsqueda, el algoritmo que genera esta búsqueda se muestra a continuación.

Código Algoritmo Hill Climbing

void hill_climbing()

{ // declaramos las variables locales

int i,h,var,salir,cont,j;

salir=0;

j=1;

var=0;

pila[1]=nodo[1][1];

revisado[1]=pila[1];

h=pila[1];

while(salir!=1) // ciclo hasta encontrar el elemento

{

i=1;

while(buscar_hijo(pila[1])!=-1) //ciclo hasta que no se encuentren

{ mas hijos

hijo[i]=buscar_hijo(pila[1]); // llena el vector hijos[]

meter_recorrido(hijo[i]); // ingresa los hijos en recorrido

i++;

}

ordenar_hijos(pila[1]); //ordena los hijos dependiendo del peso

camino_hill[j]=pila[1]; // guarda el camino

j++;

imprimir_pila(j); // imprimimos

imprimir_hijos(j);

imprimir_camino_hill(j);

sacar_cola(); //sacamos el padre de la cola

i=len_hijos();

while(1<=i)

{

meter_cola(hijo[i]); // ingresamos los hijos en la pila

i--;

}

pila[1]=hijo[1];

if(valor(camino_hill[j-1])==final) // preguntamos si encontramos

salir=1; el nodo buscado

vaciar_recorrido(); //vaciamos los vectores

vaciar_hijos();

}

}

Ejemplo del Algoritmo Hill Climbing con el programa

Para nuestro ejemplo utilizaremos 4, 2 como ciudad inicial y 3 como ciudad final.
La pantalla de ingresos de datos quedaría de la siguiente manera

Luego la matriz de peso se genera aleatoriamente y nuestro árbol de caminos quedaría de la siguiente manera.

Para la primera iteración, la pila tendría a 2 como valor inicial,
Los hijos de 2, 1-4-3, que se imprimen en forma ordenada de acuerdo a la matriz peso d[2,1] =1, d[2,4]=6, d[2,3]=59, por último el camino recorrido hasta el momento es la ciudad 2.

Para la siguiente iteración, se examinara la ciudad 1, con hijos 4 y 3 y el camino recorrido 2-1.
De la misma manera en la siguiente iteración se genera la pila hasta encontrar la ciudad objetivo, el camino optimo según el algoritmo hill climbing para nuestro ejemplo es 2 – 1 – 4 – 3, como muestra finalmente el programa

Algoritmo de A*
En general este algoritmo evita expandir aquellos caminos que ya son costosos con la utilización de heurística, con este método no se van a conseguir siempre resultados óptimos (la mejor solución), pero si se van a conseguir resultados de buena calidad en media en un tiempo razonable
Esta búsqueda se puede implementar en nuestro algoritmo como una estructura de dato tipo cola, en la cual se van guardando los hijos de los nodos revisados, así por ejemplo, se revisa primero el nodo 3, el cual se guarda en la cola.

3

0

0

0

0

Luego se revisa un hijo del nodo que no haya sido recorrido previamente
En este caso el nodo 1 y 2

2

1

0

0

0

Se ordenan los hijos del nodo 3, de acuerdo
A su heurística y recorrido y se guarda su
Recorrido con un puntero al padre.

2

1

5

0

0

Como 2 tiene de hijo al 5 se agrega
5 a abiertos

1

5

0

0

0

Luego 1 tiene hijo a 5 por lo que se consulta
Si el nuevo camino es mejor, en ese caso se cambia
El puntero del padre.

5

4

0

0

0

El algoritmo termina cuando se revisa al nodo objetivo.
Dado que para este algoritmo su estructura radica en que un nodo pueda tener más de un padre, para poder comparar los caminos, se debió crear otra estructura diferente a la utilizada a la del árbol de caminos, utilizada por el algoritmo Hill Climbing para esto se crearon las siguientes variables y funciones principales:
int heuristica[100]= me guarda el valor heurística de las ciudades

int c[100]= es vector es muy importante, ya que me guarda el camino recorrido del nodo, que lo va obteniendo gracias del puntero a los padres.
int camino[100][100]= es la matriz que guarda el puntero a los padres

int nombre_ciudades[100]= contiene las ciudades

int m_hijo[100][100]= guarda los hijos de las ciudades

int abierto[100]= vector de abiertos
int cerrado[100]= vector de cerrados

int buscar_hijo_a(int)= busca los hijos de la ciudad
int func_seleccionado(int)= retorna 1 si esta seleccionado

int valor_camino()= retorna el valor del camino recorrido mas la heurística de una ciudad

void obtener_camino(int)= llena el vector c[] con el padre actual
void obtener_camino_nuevo(int,int)= llena el vector c[] con el nuevo padre
void ordenar()= ordena de acuerdo al camino recorrido mas la heurística
Para definir la función heurística utilizamos la distancia lógica que debería existir entre 2 ciudades, por ejemplo:
Entre la ciudad 1 – 2, las separa 1 unidad de distancia lógica
Entre la ciudad 1 - 3, las separa 2 unidades de distancia lógica
Entre la ciudad 2 – 5, las separa 3 unidades de distancia lógica
Debido a que la distancia aleatoria en la matriz peso varía de 1 a 100, la distancia lógica entre 2 ciudades se multiplica por 10 para guardar las proporciones teniendo más peso en las decisiones de caminos más cortos entre distintos padres, por tanto nuestra función heurística es
Para ciudad i:

H(i)= |ciudad final - ciudad(i)|* 10

Código Búsqueda A*

void a()

{

int i,h,var,salir,cont,j,k,valor_a,valor_b,var_a;

salir=0;

j=0;

var=0;

k=0;

ingresar_abierto(nombre_ciudades[a_inicial]); //ingresamos la ciudad

Inicial a abierto

while(salir!=1)

{

i=1;

while(buscar_hijo_a(abierto[1])!=-1) // buscamos los hijos

{ //del primer elemento de abierto

hijo_a[i]=buscar_hijo_a(abierto[1]);// y los guardamos

ingresar_recorrido(hijo_a[i]); // en hijo_a[]

i++;

}

ingresar_cerrado(abierto[1]); // ingresamos el primer elemento abierto

//a cerrado

if(abierto[1]==a_final) //si encontramos la ciudad salimos

salir=1;

i=1;

while(hijo_a[i]!=-1) //para cada hijo encontrado

{

if(nuevo(hijo_a[i])==1) // si es nuevo

{

ingresar_camino(hijo_a[i],abierto[1]); //puntero al padre

ingresar_abierto(hijo_a[i]); // ingresamos a abierto

}

else

{

obtener_camino_nuevo(hijo_a[i],abierto[1]); //si no es nuevo

valor_a=valor_camino(); //obtenemos el valor de los caminos

obtener_camino(hijo_a[i]);

valor_b=valor_camino();

if(valor_a< valor_b) // si el camino nuevo es menor

{

ingresar_camino(hijo_a[i],abierto[1]); //puntero al nuevo

if(pertenece_cerrado(hijo_a[i])==1) //padre, y si

{ //pertenece a cerrado

ingresar_abierto(hijo_a[i]); // ingresamos a abierto

sacar_cerrado(hijo_a[i]); //sacamos de cerrado

}

}

}

i++;

}

sacar_abierto(); //ingresamos el primer elemento de abierto a cerrado

ordenar(); // ordenamos abierto ascendentemente

vaciar_recorrido_hijo(); // vaciamos los hijos para una nueva iteracion

}

}

Ejemplo de algoritmo A* con el programa
Para nuestro ejemplo utilizaremos la siguiente estructura:
Matriz de peso Estructura del Árbol, con ciudad
Inicial 3 y Final 5


Heurística de los nodos

Para formar esta estructura el programa nos pide como datos de entrada el número de ciudades, la ciudad inicial, la ciudad final, igual que en el algoritmo de Hill Climbing, además nos pregunta si queremos o no aplicar heurística a los nodos.
Para formar la estructura deseada, el programa nos pregunta cuantos hijos tiene el Nodo i, dependiendo del número de hijos nos preguntara cuales son estos hijos, la figura siguiente muestra como ingresar los datos para nuestro ejemplo.
En el ingreso de los datos, hay que tener la precaución de no dejar un grafo inconsistente o el algoritmo podría entrar en un ciclo infinito.
El resultado del programa se muestra en la figura.
La pantalla muestra las iteraciones del algoritmo con A = abiertos,
C = cerrados y M = N° de hijos del nodo examinado, además imprime el camino optimo y el dibujo de las ciudades visitadas.
Grafico comparativo Con y Sin heurística
Existen muchos problemas para los cuales no se conocen algoritmos que puedan encontrar la solución de forma eficiente, por lo que la solución exacta puede requerir un orden factorial o exponencial por lo que se hace necesario utilizar algoritmos heurísticos.
Un algoritmo heurístico (A*) puede producir una buena solución (puede que la óptima) pero también puede que no produzca ninguna solución o dar una solución no muy buena. Normalmente, se basa en un conocimiento intuitivo del programador sobre un determinado problema.
La heurística utilizada para nuestro trabajo se basa en la suposición que entre ciudades consecutivas el camino debiera ser mas corto, pero debido a que las distancias entre 2 ciudades se generan en forma aleatoria, la veracidad de nuestra función heurística quedará sometida al azar.
Para nuestro ejemplo utilizamos 4 estructuras elegidas al azar y para cada una de ellas se analizo con y sin heurística.

N° Ciudades	Con Herustica	Sin Heurística
4	4	4
5	6	6
6	4	3
7	4	4

Debido a que las distancias son llenadas en forma aleatoria, no se puede distinguir una tendencia del algoritmo heurístico a ser más eficiente, unas posibles mejoras a este problema sería buscar heurísticas mejores o repetir la heurística con varios orígenes; ó bien, a partir de la solución del algoritmo intentar hacer modificaciones locales para mejorar esa solución.
A pesar de esto ninguno de los dos modos de búsqueda de los algoritmos garantiza una solución óptima. Sin embargo, normalmente ambos dan soluciones buenas, incluso la óptima.

Si quieren el código, sólo tienen que pedirlo!