En este Post voy a enseñar como diseñar una red neuronal Feedforward de dos capas.
Vamos a implementar una red neuronal que permita reconocer escrituras de dígitos (0 - 9). Presentemos la red como una malla 3x5, que contiene un dibujo binario del digito.
Esta cantidad se escogió puesto que representa un mejor manera de dibujar el digito en la matriz, y además para no complicar en demasía la estructura de la red.
Configuración de la red:
nodes = 10
inputs = 15
outputs = 4
output nodes are 7-10
CONNECTIONS:
groups = 0
1-6 from i1-i15
7-10 from 1-6
selected = 1-6
weight_limit = 1.0
Diagrama de red neuronal:
Entrenamiento de la red:
Configuración archivo DATA:
| 0 | 1 |
| 111101101101111 111101000101111 111101100101111 111101101101110 011101101101111 | 010110010010010 010110010000010 010010010010010 000110010010010 001011001001001 |
| 2 | 3 |
| 111001111100111 111001111100110 111001111000111 011001111100111 111001011100111 | 111001011001111 011001011001111 111001010001111 101001011001111 110001011001111 |
| 4 | 5 |
| 101101111001001 000101111001001 001101111001001 101101101001001 101101111000001 | 111100111001111 111100111001101 111100111001110 011100111001111 111100110001111 |
| 6 | 7 |
| 111100111101111 111100111101101 111100111101110 110100111101111 111100111101011 | 111001010010010 111001011010010 011001011010010 111001010000010 111001000010010 |
| 8 | 9 |
| 111101111101111 111101111101111 101101111101111 111101010101111 111101110101111 | 111101111001111 111101111001011 011101111001111 111111111001111 111101110001111 |
Ejemplo de representación grafica de cada digito:

Configuración archivo TEACH:
0 0 0 1 = 1
0 0 1 0 = 2
0 0 1 1 = 3
0 1 0 0 = 4
0 1 0 1 = 5
0 1 1 0 = 6
0 1 1 1 = 7
1 0 0 0 = 8
1 0 0 1 = 9
Output activations
using red-10000.wts and red.data (Training Set)
0.074 0.000 0.012 0.005
0.035 0.000 0.007 0.062
0.084 0.000 0.009 0.005
0.058 0.001 0.012 0.022
0.075 0.000 0.007 0.032
0.013 0.029 0.000 0.997
0.025 0.002 0.000 0.977
0.041 0.015 0.045 1.000
0.036 0.003 0.000 0.978
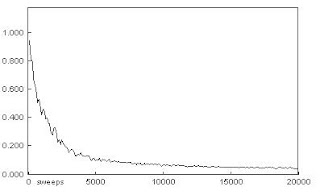
• Entrenamiento de la red con 20000 iteraciones:
Output activations
using red-20000.wts and red.data (Training Set)
0.031 0.001 0.019 0.000
0.031 0.001 0.022 0.001
0.039 0.001 0.014 0.001
0.037 0.001 0.017 0.001
0.039 0.001 0.013 0.001
0.007 0.026 0.000 1.000
0.032 0.001 0.000 1.000
0.000 0.019 0.019 1.000
0.027 0.001 0.000 1.000
0.024 0.017 0.002 0.974
111101101101100
Obteniendo como resultado los siguientes valores para 10000 y 20000 iteraciones:
using red-10000.wts and red.data (Training Set)
0.184 0.007 0.026 0.003
using red-20000.wts and red.data (Training Set)
0.009 0.007 0.009 0.004
010110000010010
Obteniendo como resultado los siguientes valores para 10000 y 20000 iteraciones:
using red-10000.wts and red.data (Training Set)
0.002 0.010 0.002 1.000
Output activations
using red-20000.wts and red.data (Training Set)
0.013 0.030 0.000 1.000
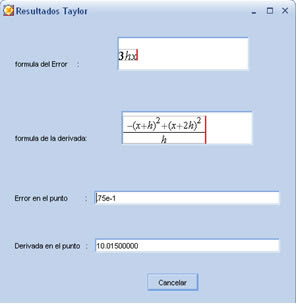
Interfaz del Software:


Código del Software:
cap1(1, 0) = -1.0992292166
cap1(1, 1) = 0.2268614322
cap1(1, 2) = 3.3533549309
‘datos entrada neurona 2.
El cálculo de los valores de las neuronas se realiza mediante la suma de la multiplicación del valor de entrada por el peso de la neurona + el peso del bias
For j = 1 To 15
valor(i) = valor(i) + cap1(i, j) * entrada(j)
Next j
Next i
‘ suma del bias que se encuentra en la posición 0 del la matriz cap1()
valor(1) = cap1(1, 0) + valor(1)
valor(2) = cap1(2, 0) + valor(2)
valor(3) = cap1(3, 0) + valor(3)
valor(4) = cap1(4, 0) + valor(4)
valor(5) = cap1(5, 0) + valor(5)
valor(6) = cap1(6, 0) + valor(6)
Finalmente se le aplica la función sigmoidea para la salida de cada neurona
For i = 1 To 6
valor(i) = sigmoidea(valor(i))
Next i
For j = 0 To 6
valor(i) = valor(i) + cap1(i, j) * valor(j)
Next j
Next i




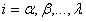 , donde
, donde 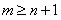 y n el orden de la derivada. Las abscisas de los puntos de la retícula son
y n el orden de la derivada. Las abscisas de los puntos de la retícula son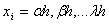 con
con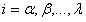 .
.
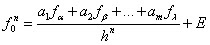
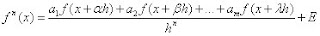 (1)
(1)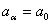 hasta
hasta 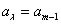 son los m coeficientes indeterminados;
son los m coeficientes indeterminados;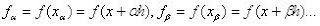 son las coordenadas que se usarán y E es el máximo error de la aproximación, que se escribe como.
son las coordenadas que se usarán y E es el máximo error de la aproximación, que se escribe como.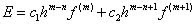 (2)
(2)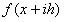 , para así calcular los coeficientes indeterminados de forma que el término E sea el máximo orden posible.
, para así calcular los coeficientes indeterminados de forma que el término E sea el máximo orden posible.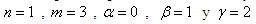
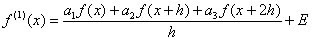 (3)
(3)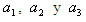 son los tres coeficientes indeterminados y
son los tres coeficientes indeterminados y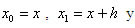
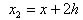 son los puntos de la retícula que se utilizarán. Sustituimos los desarrollos de
son los puntos de la retícula que se utilizarán. Sustituimos los desarrollos de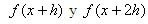 alrededor de x en la ecuación (3).
alrededor de x en la ecuación (3).

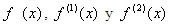 iguales a 0, 1, 0 respectivamente, debido a que el único termino existente es
iguales a 0, 1, 0 respectivamente, debido a que el único termino existente es , que es la derivada buscada, por tanto el sistema nos queda de la siguiente manera:
, que es la derivada buscada, por tanto el sistema nos queda de la siguiente manera: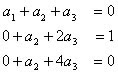

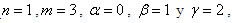 donde la derivada aproxima a cualquier función f(x) alrededor de x.
donde la derivada aproxima a cualquier función f(x) alrededor de x.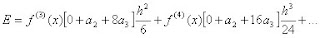
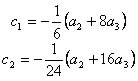
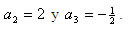


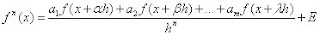
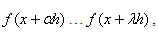 , donde
, donde 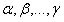 son los m puntos, estos puntos necesitaremos almacenarlos en un vector que llamaremos V[m] de largo m, quedando:
son los m puntos, estos puntos necesitaremos almacenarlos en un vector que llamaremos V[m] de largo m, quedando: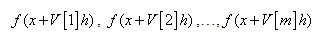

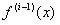 los cuales corresponden a los argumentos principales, y las columnas corresponden a los a
los cuales corresponden a los argumentos principales, y las columnas corresponden a los a
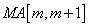 .
.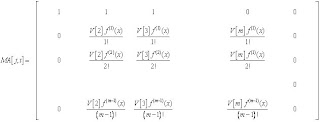

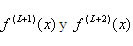 se expresa:
se expresa: