Si tenemos m puntos en un sub – intervalo, enumerados en 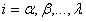 , donde
, donde 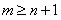 y n el orden de la derivada. Las abscisas de los puntos de la retícula son
y n el orden de la derivada. Las abscisas de los puntos de la retícula son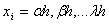 con
con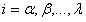 .
.
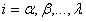 , donde
, donde 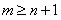 y n el orden de la derivada. Las abscisas de los puntos de la retícula son
y n el orden de la derivada. Las abscisas de los puntos de la retícula son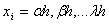 con
con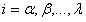 .
.
Por tanto la aproximación por diferencias de la derivada de orden n conm puntos se expresa:
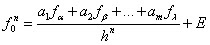
O bien.
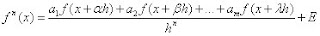 (1)
(1)En donde 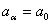 hasta
hasta 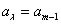 son los m coeficientes indeterminados;
son los m coeficientes indeterminados;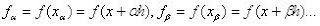 son las coordenadas que se usarán y E es el máximo error de la aproximación, que se escribe como.
son las coordenadas que se usarán y E es el máximo error de la aproximación, que se escribe como.
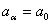 hasta
hasta 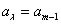 son los m coeficientes indeterminados;
son los m coeficientes indeterminados;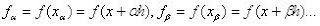 son las coordenadas que se usarán y E es el máximo error de la aproximación, que se escribe como.
son las coordenadas que se usarán y E es el máximo error de la aproximación, que se escribe como.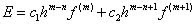 (2)
(2)Una vez obtenido la formula (1) de aproximación por diferencias dado un orden n y m puntos, se sustituye en esta ecuación por los desarrollos de Taylor de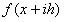 , para así calcular los coeficientes indeterminados de forma que el término E sea el máximo orden posible.
, para así calcular los coeficientes indeterminados de forma que el término E sea el máximo orden posible.
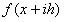 , para así calcular los coeficientes indeterminados de forma que el término E sea el máximo orden posible.
, para así calcular los coeficientes indeterminados de forma que el término E sea el máximo orden posible.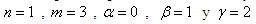 . Entonces la ecuación (1) queda.
. Entonces la ecuación (1) queda.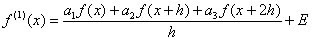 (3)
(3)En donde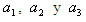 son los tres coeficientes indeterminados y
son los tres coeficientes indeterminados y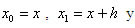
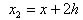 son los puntos de la retícula que se utilizarán. Sustituimos los desarrollos de
son los puntos de la retícula que se utilizarán. Sustituimos los desarrollos de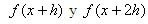 alrededor de x en la ecuación (3).
alrededor de x en la ecuación (3).
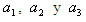 son los tres coeficientes indeterminados y
son los tres coeficientes indeterminados y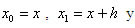
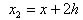 son los puntos de la retícula que se utilizarán. Sustituimos los desarrollos de
son los puntos de la retícula que se utilizarán. Sustituimos los desarrollos de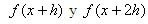 alrededor de x en la ecuación (3).
alrededor de x en la ecuación (3).
Reagrupando…
La ecuación (4) contiene tres coeficientes indeterminados, los cuales se pueden definir mediante tres condiciones formando un sistema. Para minimizar el error de la ecuación (4), hacemos los coeficientes de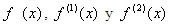 iguales a 0, 1, 0 respectivamente, debido a que el único termino existente es
iguales a 0, 1, 0 respectivamente, debido a que el único termino existente es , que es la derivada buscada, por tanto el sistema nos queda de la siguiente manera:
, que es la derivada buscada, por tanto el sistema nos queda de la siguiente manera:
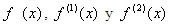 iguales a 0, 1, 0 respectivamente, debido a que el único termino existente es
iguales a 0, 1, 0 respectivamente, debido a que el único termino existente es , que es la derivada buscada, por tanto el sistema nos queda de la siguiente manera:
, que es la derivada buscada, por tanto el sistema nos queda de la siguiente manera: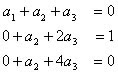 (5)
(5)Una vez resuelto el sistema anterior obtendremos los valores de los tres coeficientes indeterminados, los cuales son:
Una vez encontrado estos valores se sustituyen en la ecuación (3) y obtendremos finalmente la ecuación por diferencias para nuestro caso en particular, donde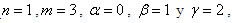 donde la derivada aproxima a cualquier función f(x) alrededor de x.
donde la derivada aproxima a cualquier función f(x) alrededor de x.
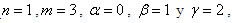 donde la derivada aproxima a cualquier función f(x) alrededor de x.
donde la derivada aproxima a cualquier función f(x) alrededor de x.Por otro lado, los términos no nulos de la ecuación (4) constituyen el error.
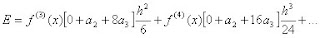 (6)
(6)Al comparar las ecuaciones (2) y (6) obtenemos que:
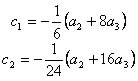
De lo que se obtiene, sustituyendo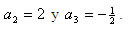
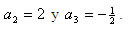
Debido a que el primer término del error no es nulo, ecuación (6), ignoramos el segundo término y escribimos el término del error como:
En el caso en que el primer término del error se anule, el segundo término pasará a representar el error.
Resolución del algoritmo genérico en Maple
Una vez planteado el fundamento teórico del algoritmo genérico para la obtención de formulas de aproximación por diferencia de una derivada de orden n, desarrollaremos un programa basado en Maple que nos permita utilizar dicho método.
Basándonos en m como el número de puntos en la retícula y con n como orden de la derivada, nos basaremos en la siguiente ecuación.
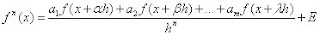
Donde utilizaremos los desarrollos de Taylor para los m términos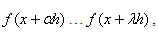 , donde
, donde 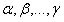 son los m puntos, estos puntos necesitaremos almacenarlos en un vector que llamaremos V[m] de largo m, quedando:
son los m puntos, estos puntos necesitaremos almacenarlos en un vector que llamaremos V[m] de largo m, quedando:
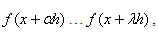 , donde
, donde 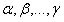 son los m puntos, estos puntos necesitaremos almacenarlos en un vector que llamaremos V[m] de largo m, quedando:
son los m puntos, estos puntos necesitaremos almacenarlos en un vector que llamaremos V[m] de largo m, quedando: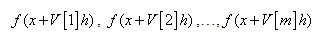
Donde cada uno de estos elementos se reemplaza por la serie de Taylor correspondiente, donde se almacenaran en una columna de una matriz, quedando de la siguiente manera:
Cada termino de Taylor se truncara hasta el termino m, donde los términos m + 1 y m + 2
Se utilizaran para el cálculo de error, nótese que en la matriz sólo se almacena el término que acompaña a cada derivada de la serie.
Con lo que podemos observar que cada fila corresponde al argumento 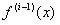 los cuales corresponden a los argumentos principales, y las columnas corresponden a los a1,…,aL que serán los argumentos a agrupar.
los cuales corresponden a los argumentos principales, y las columnas corresponden a los a1,…,aL que serán los argumentos a agrupar.
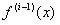 los cuales corresponden a los argumentos principales, y las columnas corresponden a los a1,…,aL que serán los argumentos a agrupar.
los cuales corresponden a los argumentos principales, y las columnas corresponden a los a1,…,aL que serán los argumentos a agrupar.Con esta idea podremos construir nuestro sistema de ecuaciones, multiplicando por el coeficiente propio de la formula anterior y ampliando nuestra matriz a 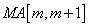 .
.
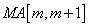 .
.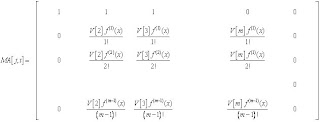

Ahora generaremos el código Maple para poder ingresar estos valores descritos a la matriz MA [ ] Procedimiento para ingresar valores a la matriz MA [].
For i from 1 to m do
For j from 1 to m do
MA [j,i]:=(V[i]*h)^(j-1)/(j-1)!*(1/h^n);
od;
od;
MA [n+1,m+1]:=1;
En donde la matriz que contiene los coeficientes de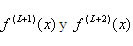 se expresa:
se expresa:
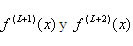 se expresa:
se expresa:En donde los términos del error se guardan en un vector e[] de dimensión 2 :
Procedimiento para ingresar los valores al vector e[]
V[1]:=0: V[2]:=1: V[3]:=2;
e[1]:=0;
e[2]:=0;
For i from m+1 to m+2 do
For j from 1 to m do
e[i-m]:=e[i-m]+a[j]*(V[j]*h)^(i-1)/(i-1)!*(1/h^n);
od;
od;
Una vez ingresadas las dos matrices se procede a su cálculo, para calcular la matriz MA[]
utilizaremos el comando LinearSolve, de la siguiente manera
a:=LinearSolve(MA);
Para calcular la expresión del error comprobamos si el primer término es nulo
if e[1]=0 then;
E=e[2]*(D@@L)(f);
else;
E=e[1]*(D@@L)(f);
end if;
Utilización del programa
Para comenzar a utilizar el programa se debe ingresar la instrucción Maplets[Display](maplet), esta instrucción mostrarla pantalla de presentación
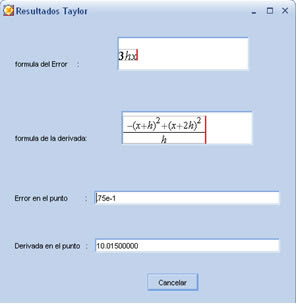
Que nos dara la opción de ir a la ventana de entrada de valores, esta ventana nos dara la opción de ingresar los valores de la derivada, los puntos la función, y el valor del h que por defecto es 0.005, luego nos salimos de la ventana de ingreso de valores y con el comando, Maplets[Display](mostrar):, inicializamos la ventana de los resultados,
que mostrara la formula de error y derivada, y la evaluación en los puntos correspondientes.ahí va el código completo.....
Diferenciación Numérica Polinomios de Taylor
> restart;
> with(LinearAlgebra):
> AproxDiferencia:= proc(p,L,LI,F,X,H)
> local i,j,expresion,E,B,e,a,f,fp,fe,po,po1;
> B:=Matrix(L,L+1);
> e:=Vector(2); # Verctor de coeficientes de error
>
> for i from 1 to L do
> for j from 1 to L do
> B[j,i]:=(LI[i]*h)^(j-1)/(j-1)!*(1/h^p); # 'LI' es el valor del punto de la reticula
> od;
> od;
> B[p+1,L+1]:=1;
> a:=LinearSolve(B);
>
> f:=unapply(F,x);
> expresion:=sum('a[k]*f(x+LI[k]*h)','k'=1..L)/h^p;
> e[1]:=0;
> e[2]:=0;
> for i from L+1 to L+2 do
> for j from 1 to L do
> e[i-L]:=e[i-L]+a[j]*(LI[j]*h)^(i-1)/(i-1)!*(1/h^p); # 'LI' es el valor del punto de la reticula
> od;
> od;
> if e[1]=0 then;
> E:=e[2]*diff(f(x),x$p);;
> else;
> E:=e[1]*diff(f(x),x$p);;
> end if;
> fp:=unapply(expresion,x,h); Maplets:-Tools:-Set( 'visor' = MathML[Export](expresion));
> fe:=unapply(E,x,h); Maplets:-Tools:-Set( 'visor2' = MathML[Export](E));
> po:=fp(X,H);Maplets:-Tools:-Set( 'TF9' = evalf(po) );
> po1:=fe(X,H);Maplets:-Tools:-Set( 'TF10' = evalf(po1) );
> print(evalf(po));
> print(evalf(po1));
> print(E);
>
>
> end proc:
> with(Maplets[Elements]):maplet1:= Maplet([["Orden de la Derivada: ", TextField['TF1'](5)],
> ["Numero de Puntos: ", TextField['TF2'](5)],
> ["Puntos: ",TextField['TF3']("\[,\]",10)],
> ["Funcion: ",TextField['TF4'](10)],
> ["Punto a evaluar - x:",TextField['TF5'](8)],
> ["Amplitud h: ",TextField['TF6']("0.005", 10)],
> ["Ecuacion de la Derivada: "],
> [MathMLViewer( 'reference'='visor')],
> ["Error: "],
> [MathMLViewer( 'reference'='visor2')],
> ["Valor Derivada: ",TextField['TF9'](10)],
> ["Valor Eror: ",TextField['TF10'](10)],
> [Button("Derviar por Diferencias", Evaluate('function' = 'AproxDiferencia(TF1,TF2,TF3,TF4,TF5,TF6)')), Button("Salir", Shutdown(['TF1']))
> ]]):
> Maplets[Display](maplet1);














1 comentario:
Buenas noches, muy interesante tu post, no tendras el codigo en matlab ?
Publicar un comentario